你的背包，让我走的好缓慢

动态规划，01背包问题

背包问题是经典的动态规划问题，这里先说一下简单的01背包

问题是这样的：

一共有N件物品，第i（i从1开始）件物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够装入背包的最大价值是多少？

最简单的思路就是，枚举所有情况，每个物品都有放或者不放两种情况，那N个物品，就是2^N种情况，数量级直接爆炸。

动态规划的思想就是能不能利用子问题的解，来求解当前问题

现在有个实例，物品个数n=3，背包容量w=5，重量数组weights={2,4,1}, 价值数组values={10,5,4}

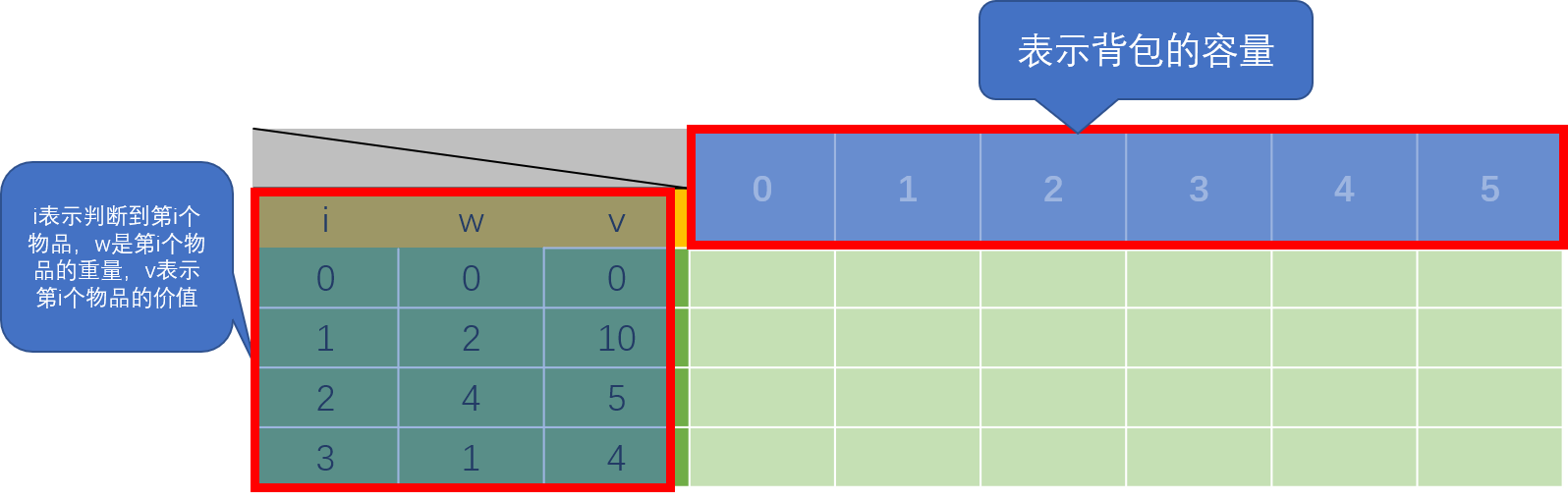
假设dp[n][w]表示前N个物体装入w容量的背包能装入的最大价值，构成一个二维表，dp的过程就是填表的过程

构建一个二维表来填空，其中列表示容量，行表示第i个物品，所以对应的重量和价值数组需要对应下标为i-1

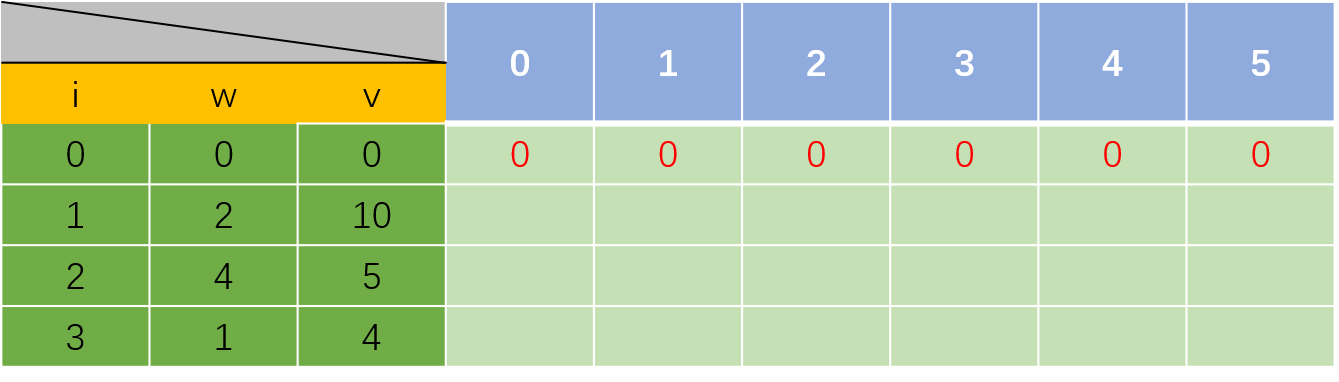
对于边界条件，第0个物品，也就是没有物品可放时，有再多的容量也没用，所以对应的价值都为0

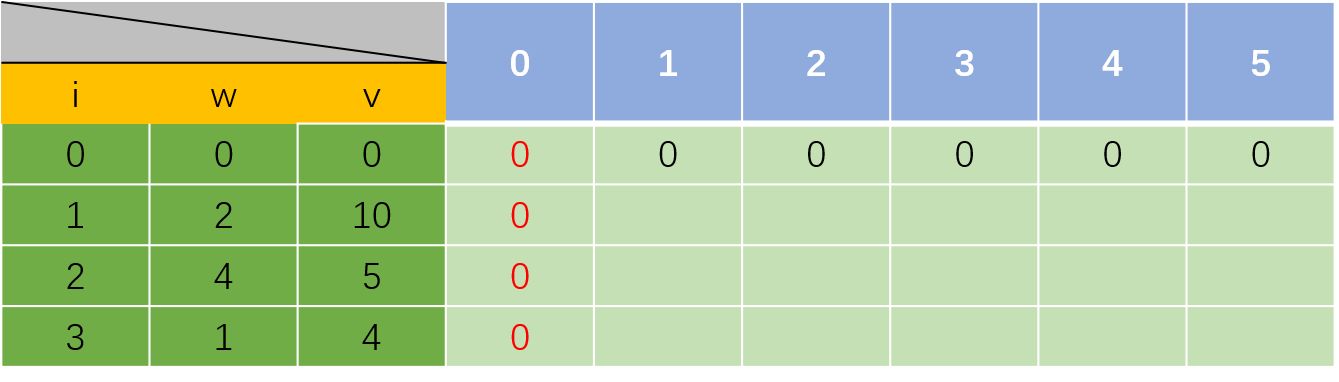
同样的，当容量为0时，有再多的物品也没用，对应的价值都为0

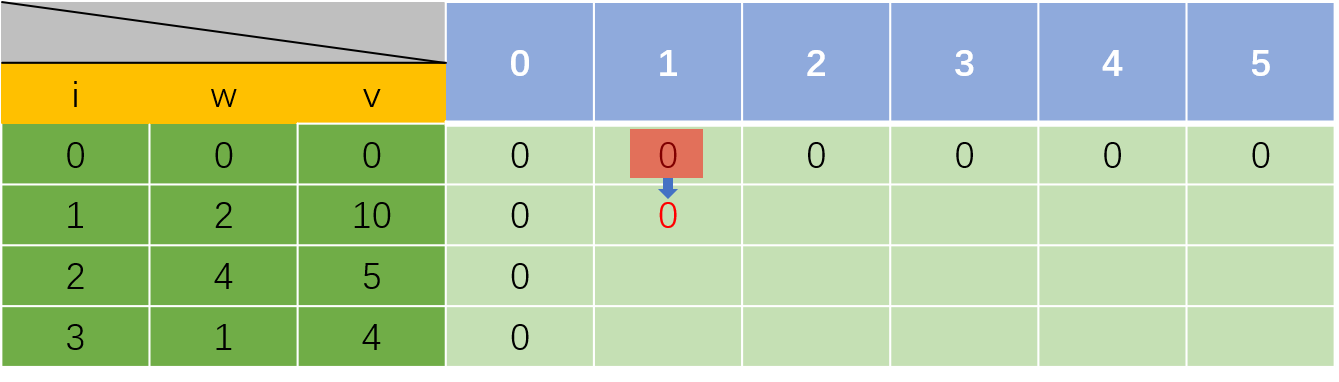
那从dp[1][1]开始填表，

第一个物品，如果他的重量大于当前容量，就不考虑放进去，所以和上一个物品判断的结果一样，则dp[i][j]=dp[i-1][j]；

如果他的重量小于等于当前容量，可以考虑放进去或者不放进去，就出现了两种情况，需要选取两种情况的最大值，若不放进去就是dp[i][j]=dp[i-1][j]，如果放进去，当前容量为j-weights[i-1]，再加上当前物品的价值values[i-1]，即dp[i][j]=max(dp[i-1][j], dp[i-1][j-weights[i-1]]+values[i-1])

在这里，物品重量是大于当前容量的，所以遵循dp[i][j]=dp[i-1][j]，找到dp[0][1]

这里也是一样的

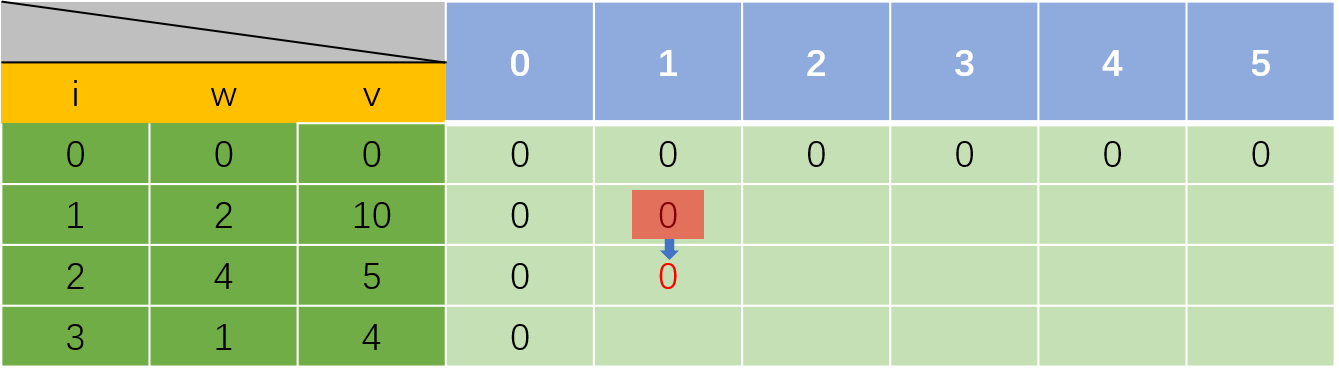
到这里，物品重量等于容量的，所以需要找到dp[i-1][j]和dp[i-1][j-weights[i-1]]+values[i-1]两个数值进行对比，在这里就是dp[2][1]和dp[2][0]+4，

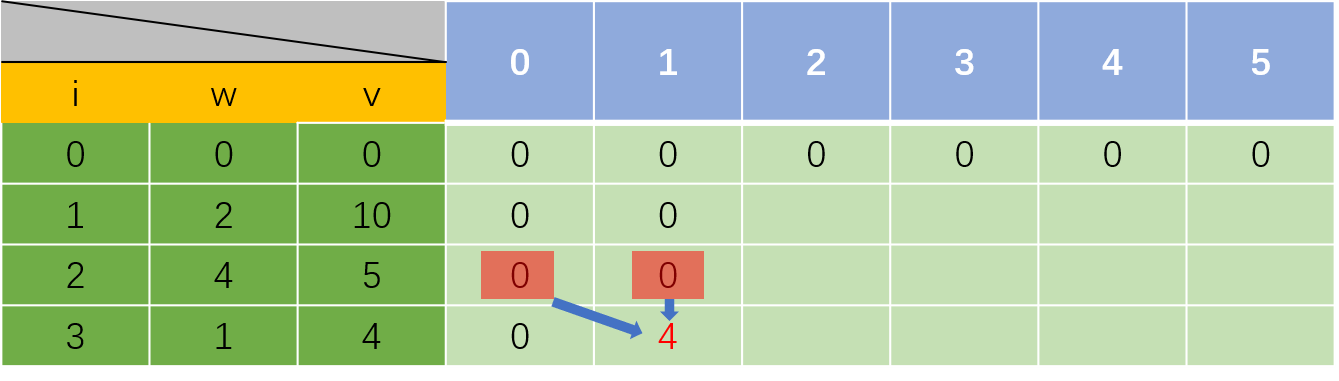
其他的元素以此类推，填满整个二维表

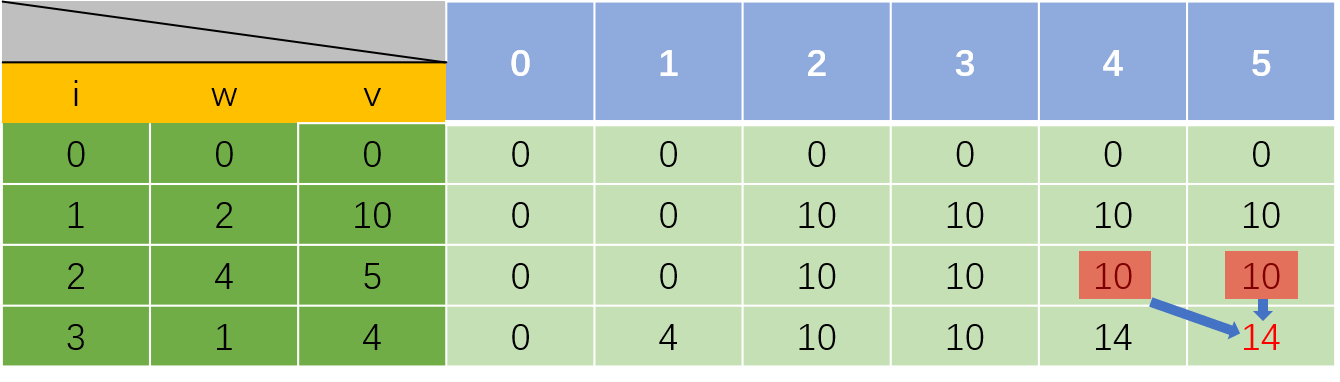
至此，dp[n][w]即为最大价值。

代码为：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int main() {
    int n=3;
    int w = 5;
    vector<int> weights = { 2,4,1 };
    vector<int> values = { 10,5,4 };
    vector<vector<int>> dp(n+1, vector<int>(w+1,0));

    for (int i = 0; i < n+1; i++) dp[i][0] = 0;
    for (int j = 0; j < w+1; j++) dp[0][j] = 0;

    for (int i = 1; i < n+1; i++) {
        for (int j = 1; j < w + 1; j++) {
            if (j > weights[i - 1]) {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1]);
            }
            else dp[i][j] = dp[i - 1][j];
        }
    }

    for (int i = 0; i < n + 1; i++) {
        for (int j = 0; j < w + 1; j++) {
            cout << dp[i][j] << " ";
        }
        cout << endl;
    }

    cout << dp[n][w];
}

到这里二维的dp过程就结束了，其实我们观察一下，会发现，对于每一列，其实我们只关心每一个书包容量下能装下的最大价值，所以我们只需要保存每一列的最大值即可，所以将二维的dp转为一维的dp

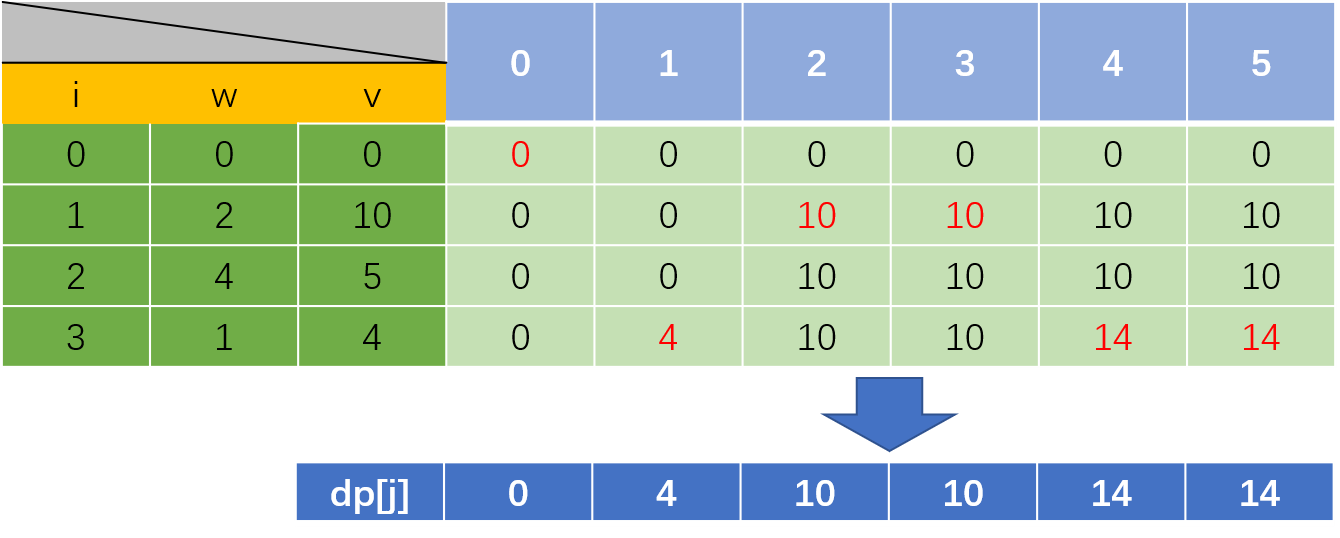
dp方程也改为dp[j]=max(dp[j],dp[j-weights[i-1]]+values[i-1])

代码为：

int main() {
    int n = 3;
    int w = 5;
    vector<int> weights = { 2,4,1 };
    vector<int> values = { 10,5,4 };
    vector<int> dp(w + 1, 0);

    for (int i = 1; i < n + 1; i++) {
        for (int j = w; j > 1; j--) {
            if (j >= weights[i - 1]) {
                dp[j] = max(dp[j], dp[j - weights[i - 1]] + values[i - 1]);
            }
        }
    }

    for (int j = 0; j < w + 1; j++) {
        cout << dp[j] << " ";
    }

    cout <<endl<< dp[w];
}

这里要注意下j遍历的顺序，这个挺重要的

好的，今天就到这里了，下一次会介绍01背包引申出来的题目

参考链接
https://zhuanlan.zhihu.com/p/93857890

https://www.nowcoder.com/questionTerminal/2820ea076d144b30806e72de5e5d4bbf

https://www.nowcoder.com/questionTerminal/fd55637d3f24484e96dad9e992d3f62e?answerType=1&f=discussion